Numbers can have interesting patterns.
Here we list the most common patterns and how they are made.
Arithmetic Sequences
An Arithmetic Sequence is made by adding some value each time.
Examples:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
The pattern is continued by adding 3 to the last number each time.
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
The pattern is continued by adding 5 to the last number each time.
The value added each time is called the "common difference"
What is the common difference in this example?
| 19, 27, 35, 43, ... |
Answer: The common difference is 8
The common difference could also be negative, like this:
| 25, 23, 21, 19, 17, 15, ... |
The pattern is continued by subtracting 2 each time.
Geometric Sequences
A Geometric Sequence is made by multiplying by some value each time.
Examples:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
The pattern is continued by multiplying the last number by 2 each time.
| 3, 9, 27, 81, 243, 729, 2187, ... |
The pattern is continued by multiplying the last number by 3 each time.
Special Sequences
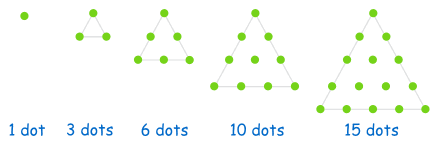
Triangular Numbers
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
This sequence is generated from a pattern of dots which form a triangle.
By adding another row of dots and counting all the dots we can find the next number of the sequence:
Square Numbers
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
The next number is made by squaring where it is in the pattern.
The second number is 2 squared (22 or 2×2)
The seventh number is 7 squared (72 or 7×7) etc
Cube Numbers
1, 8, 27, 64, 125, 216, 343, 512, 729, ...
The next number is made by cubing where it is in the pattern.
The second number is 2 cubed (23 or 2×2×2)
The seventh number is 7 cubed (73 or 7×7×7) etc
Fibonacci Numbers
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
The next number is found by adding the two numbers before it together.
The 2 is found by adding the two numbers in front of it (1+1)
The 21 is found by adding the two numbers in front of it (8+13)
The next number in the sequence above would be 55 (21+34)
 DISCUSSION
GROUP
DISCUSSION
GROUP



Write a comment